Google Code Jam Round1A "Number"
by 小伟
Google Code Jam Round1A "Number"
题目描述:给定一个数n(2 <= n <= 2000000000),求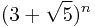 的整数部分最后三位。
的整数部分最后三位。
For example, when n = 5, 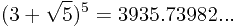 The answer is 935.
The answer is 935.
解法:
1. 直接求,要求精度高,当n>28时,结果就出错。
2. 技巧解法,配数法:
首先设
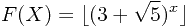
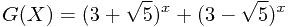
把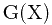 展开,得到:
展开,得到:
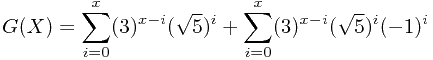
展开后发现,包含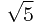 的项都相互抵消了,得到:
的项都相互抵消了,得到:
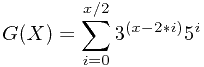
从上式中可以看出,G(X)是整数。
由于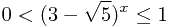 ,因此
,因此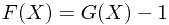 。
。
于是问题就转化为求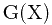 ,求
,求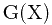 也是使用配数法,如下:
也是使用配数法,如下:
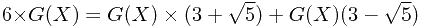
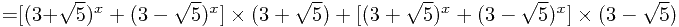
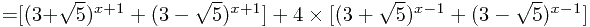
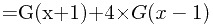
因此,得到递推公式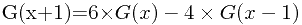
由于题目中的n值较大,不能直接使用递推公式,我们可以构造一个矩阵来加速求解:
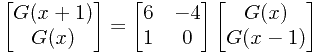
其中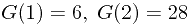 ,所以
,所以
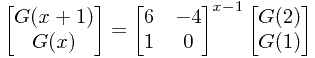
使用按位乘法,就可以在Log(x)的复杂度内,求出G(X)。
至此,本题顺利解决。
World Final 2008 Problem B -- 判断多项式恒被整除
by F.Yang
ACM/ICPC World Final 2008 Problem B 给定整系数多项式  及正整数
及正整数 . 判断对
. 判断对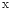 取遍所有整数,
取遍所有整数,  是否恒被
是否恒被 整除.
整除.
分析 我们先定义一些概念.
定义1 设 为整系数多项式,
为整系数多项式,  为非零整数, 若对任意
为非零整数, 若对任意 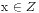 , 都有
, 都有 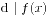 . 我们则称
. 我们则称  恒被
恒被  整除.
整除.
定义2 记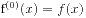 ,
, 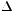 为向前差分算子, 定义n 阶差分多项式(简称n 阶差分)
为向前差分算子, 定义n 阶差分多项式(简称n 阶差分)
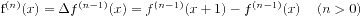 .
.
我们有如下定理.
定理1 整系数多项式  恒被
恒被 整除, 当且仅当
整除, 当且仅当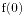 被
被 整除, 且
整除, 且 的一阶差分
的一阶差分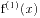 恒被
恒被 整除.
整除.
证明 充分性. 因为 恒被
恒被 整除, 所以
整除, 所以 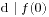 ,
, 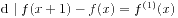 (
(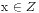 ). 充分性得证.
). 充分性得证.
必要性. 使用数学归纳法. 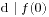 . 设对非负整数数
. 设对非负整数数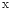 , 都有
, 都有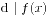 . 又因为
. 又因为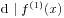 , 故
, 故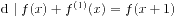 . 同理, 设对整数
. 同理, 设对整数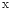 , 有
, 有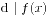 . 则
. 则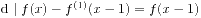 . 综合上述, 由数学归纳法知, 必要性得证.
. 综合上述, 由数学归纳法知, 必要性得证. 
定理2 设整系数多项式 的次数为
的次数为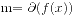 , 则
, 则 恒被非零整数
恒被非零整数 整除, 当且仅当
整除, 当且仅当 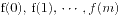 均被
均被 整除.
整除.
证明 充分性是显然的.
必要性的证明施归于纳多项式的次数m. 当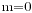 , 即
, 即 为常数时, 结论显然成立. 设
为常数时, 结论显然成立. 设 时结论成立. 则对
时结论成立. 则对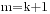 次多项式
次多项式 , 若
, 若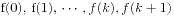 均被
均被 整除, 则
整除, 则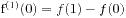 ,
, 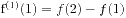 , ... ,
, ... , 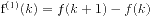 均能被
均能被 整除。又有
整除。又有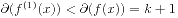 . 由归纳假设知, 一阶差分
. 由归纳假设知, 一阶差分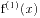 恒被
恒被 整除. 又根据定理1, 得知
整除. 又根据定理1, 得知 恒被
恒被 整除. 由数学归纳法, 必要性得证.
整除. 由数学归纳法, 必要性得证. 
定理3 设整系数多项式 的次数为
的次数为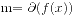 , 则
, 则 恒被非零整数
恒被非零整数 整除, 当且仅当对任意连续m+1个整数
整除, 当且仅当对任意连续m+1个整数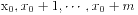 , 有
, 有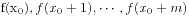 均被
均被 整除.
整除.
定理3作为定理2的推广, 证明方法也是类似的, 此处从略.
推论1 设整系数多项式 的次数为
的次数为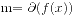 ,
, 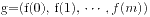 ,
,  恒被
恒被 整除当且仅当
整除当且仅当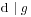 .
.
至此,整个问题得到完整解决.
CII2187-一般任务安排问题的最小费用最大流解法及其他
by F.Yang
CII-2187问题描述:一人以看录像维生. 每个录像有三个属性 (s, f, p) 分别表示该任务的开始时间,结束时间和所得收入. 但这个人在同一时刻最多只能看两个录像. 现给定 n 个录像. 问这个人的最大收入是多少.
分析: 我们把问题一般化, 设这个人在同一时刻最多能看 k 个电影. 我们使用最小费用最大流来解决这个问题.
把每个任务的开始时间和结束时间都对应设为图的一个顶点. 对每个任务 (s, f, p), s 结点到 f 结点连一条弧, 容量为1, 费用为 -p. 而对任意两个任务(si, fi, pi), (sj, fj, pj), 如果fi<=sj, 则从 fi 到 sj 连一条弧, 容量为1, 费用为0. 设一超级源 R0, R0 到各个任务的开始时间 si 都连一条容量为1, 费用为0的弧. 再设一超超级源 R1, R1仅有到R0容量为k, 费用为0的弧. 最后设一超级汇 R2, 各任务的结束时间 fi 到R2都有一条容量为1, 费用为0的弧.
求从 R1 到 R2 的最小费用最大流, 得到费用 cost, 则 -cost 即为问题的答案.
讨论: 虽然上述算法在一般化的角度解决了这个问题, 但是由于解决费用流的算法复杂度约为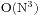 , 这在某些有特殊限制的问题变种里并不见得是一种首选的高效算法. 现在总结一下一些特殊的变种及适合的方法.
, 这在某些有特殊限制的问题变种里并不见得是一种首选的高效算法. 现在总结一下一些特殊的变种及适合的方法.
(1) 单资源无费用. 如果上题那个人任一时刻只能看一个录像, 并且每看一个录像的收入都是1, 那么这是一个经典的活动安排问题. 任务按结束时间排序后使用贪心算法即可解决. 算法的时间复杂度为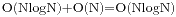 .
.
(2) 单资源有费用. 如果上题观看者每一时刻都只能看一个录像. 任务按结束时间排序后使用一个DP即可, 设 dp[i] 表示以任务 i 结束的情况下所能获得的最大收益. 该算法的时间复杂度为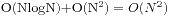 .
.
(3) 多资源无费用. 如果上题里观看者每一时刻最多可以看k个录像, 但是看每个录像的收入都是1. 可以使用如下算法解决:
a. 维护一个数据结构T, 表示各个资源的最后可用时间, 初始时里面有k个0;
b. 将任务按结束时间排序;
c. 顺序扫描每个任务 (s, f), 在 T 里面查找一个不大于 s 的最大的元素 t. 如果能找到, 则选取该任务, 并将 t 更新为 f 加入回 T 中, 若不能找到 t, 则放弃该任务.
T使用平衡树来维护, 每次查找和更新的复杂度为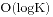 , 整个算法的复杂度为
, 整个算法的复杂度为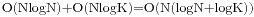 . 但编码的复杂度很大.
. 但编码的复杂度很大.
(4) 两资源有费用. 这即为原题本身. 可以使用两维状态的三方dp来解决. 小伟已经使用该方法通过了该题. 呼唤小伟给出算法详解和代码.
PKU1031-求点对多边形所成张角
by F. Yang
PKU1031题意描述:在坐标原点处有一个点光源S. 在距离S为r处的亮度为
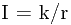 ,
,
其中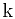 为与光源有关的常数. 而光对在某处一高度为
为与光源有关的常数. 而光对在某处一高度为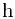 长度为
长度为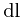 的小量竖直矩形的照度为
的小量竖直矩形的照度为
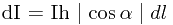 ,
,
其中 为该小量矩形处的亮度,
为该小量矩形处的亮度,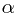 为光源到
为光源到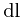 处的方向与
处的方向与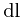 的法线方向的夹角.
的法线方向的夹角.
现有一高度为 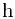 的简单多边形篱笆,用点列
的简单多边形篱笆,用点列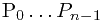 描述. 原点不在多边形的边上. 求光源对多边形各处的照度的总和.
描述. 原点不在多边形的边上. 求光源对多边形各处的照度的总和.
分析: 设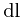 的两端点为A, B. 且A, B在光源S到直线AB的垂足的同侧, 否则只需要将AB从垂足处分为两条线段讨论即可. 另外假设A离垂足较近. 设S到AB的垂线与SA的夹角为
的两端点为A, B. 且A, B在光源S到直线AB的垂足的同侧, 否则只需要将AB从垂足处分为两条线段讨论即可. 另外假设A离垂足较近. 设S到AB的垂线与SA的夹角为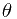 , 而S到AB的小量张角为
, 而S到AB的小量张角为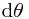 . SA的长度为
. SA的长度为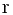 . 由小量分析的方法可得
. 由小量分析的方法可得
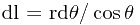 .
.
易知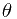 即为上述的
即为上述的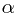 . 故得到在
. 故得到在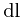 处的照度为
处的照度为
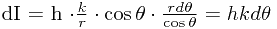 .
.
显然,照度与距离无关,只与张角有关. 故这个问题变成求一个点对一个简单多边形的张角.
求点对多边形张角的问题可以用投影和区间并的思想解决:
(1) 令 ;
;
(2 )维护一个闭区间序列ints[], 初始为空;
(3) 对每条条线段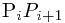 ,
, 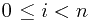 , 求出向量
, 求出向量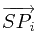 和
和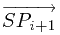 的辐角
的辐角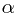 ,
, 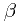 , 设
, 设 . 若
. 若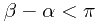 , 则将区间
, 则将区间![[\alpha, \beta] [\alpha, \beta]](http://matrix.is-programmer.com/user_files/Matrix/epics/2f4819f67192844c5777233fcba753b45378a64d.png) 加入到序列ints[]中, 否则分别将区间
加入到序列ints[]中, 否则分别将区间![[0, \alpha] [0, \alpha]](http://matrix.is-programmer.com/user_files/Matrix/epics/d3df8d55edf31aea0efcdf495bb0f072428ef4d6.png) ,
, ![[\beta, 2\pi] [\beta, 2\pi]](http://matrix.is-programmer.com/user_files/Matrix/epics/366a660a7f4ef9b35c01ce93bc1efe8873352478.png) 加入到序列ints[]中.
加入到序列ints[]中.
(4) 将区间序列ints[]按左端排序, 合并各个相交的区间;
(5) 最后剩下的不相交区间的长度总和就是所求夹角.
下面为解决这个问题的代码, 函数接口为double angfun(pt p[], int n) , 由于本题光源刚好在原点,所以不当作参数, 对其他点也是容易处理的, 坐标平移一下即可.
-
struct pt{
-
double x, y;
-
};
-
-
struct interval{
-
double a, b;
-
};
-
-
const double pi=acos(-1.0);
-
-
bool cmp(interval s1, interval s2)
-
{
-
return s1.a<s2.a || s1.a==s2.a && s1.b<s2.b;
-
}
-
-
double angle(pt p)
-
{
-
double r, alpha;
-
-
r=sqrt(p.x*p.x+p.y*p.y);
-
alpha=acos(p.x/r);
-
if(p.y<0) alpha=2*pi-alpha;
-
return alpha;
-
}
-
-
double angfun(pt p[], int n)
-
{
-
int i, m=0, t;
-
interval s[110];
-
double a, b, total;
-
-
p[n]=p[0];
-
-
for(i=0; i<n; i++){
-
a=angle(p[i]);
-
b=angle(p[i+1]);
-
if(a>b) swap(a, b);
-
if(b-a<pi-eps){
-
s[m].a=a;
-
s[m].b=b;
-
m++;
-
}
-
else{
-
s[m].a=0;
-
s[m].b=a;
-
m++;
-
s[m].a=b;
-
s[m].b=2*pi;
-
m++;
-
}
-
}
-
-
sort(s, s+m, cmp);
-
-
t=0;
-
for(i=1; i<m; i++)
-
if(s[i].a<=s[t].b){
-
if(s[t].b<s[i].b) s[t].b=s[i].b;
-
}
-
else s[++t]=s[i];
-
-
total=0;
-
for(i=0; i<=t; i++) total+=s[i].b-s[i].a;
-
-
return total;
-
}
-
讨论: 假设允许点在多边形上, 这个方法也是可用的, 不过我们需要知道这个时候点是看作影响多边形外还是影响多边形内. 另外还需要判断每条边的左侧是内部还是右侧是内部. 这只要按叉积求一次面积即可判断. 具体在此从略. 本部分感谢bigheadghost提示.
PS: PKU上该题做成多case会wrong到死, 要做成单case才能过, 晕死!
