PKU1031-求点对多边形所成张角
by F. Yang
PKU1031题意描述:在坐标原点处有一个点光源S. 在距离S为r处的亮度为
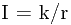 ,
,
其中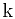 为与光源有关的常数. 而光对在某处一高度为
为与光源有关的常数. 而光对在某处一高度为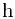 长度为
长度为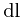 的小量竖直矩形的照度为
的小量竖直矩形的照度为
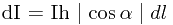 ,
,
其中 为该小量矩形处的亮度,
为该小量矩形处的亮度,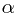 为光源到
为光源到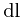 处的方向与
处的方向与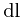 的法线方向的夹角.
的法线方向的夹角.
现有一高度为 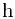 的简单多边形篱笆,用点列
的简单多边形篱笆,用点列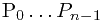 描述. 原点不在多边形的边上. 求光源对多边形各处的照度的总和.
描述. 原点不在多边形的边上. 求光源对多边形各处的照度的总和.
分析: 设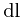 的两端点为A, B. 且A, B在光源S到直线AB的垂足的同侧, 否则只需要将AB从垂足处分为两条线段讨论即可. 另外假设A离垂足较近. 设S到AB的垂线与SA的夹角为
的两端点为A, B. 且A, B在光源S到直线AB的垂足的同侧, 否则只需要将AB从垂足处分为两条线段讨论即可. 另外假设A离垂足较近. 设S到AB的垂线与SA的夹角为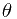 , 而S到AB的小量张角为
, 而S到AB的小量张角为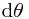 . SA的长度为
. SA的长度为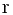 . 由小量分析的方法可得
. 由小量分析的方法可得
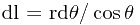 .
.
易知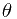 即为上述的
即为上述的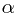 . 故得到在
. 故得到在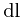 处的照度为
处的照度为
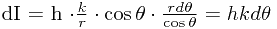 .
.
显然,照度与距离无关,只与张角有关. 故这个问题变成求一个点对一个简单多边形的张角.
求点对多边形张角的问题可以用投影和区间并的思想解决:
(1) 令 ;
;
(2 )维护一个闭区间序列ints[], 初始为空;
(3) 对每条条线段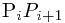 ,
, 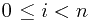 , 求出向量
, 求出向量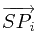 和
和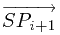 的辐角
的辐角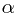 ,
, 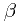 , 设
, 设 . 若
. 若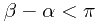 , 则将区间
, 则将区间![[\alpha, \beta] [\alpha, \beta]](http://matrix.is-programmer.com/user_files/Matrix/epics/2f4819f67192844c5777233fcba753b45378a64d.png) 加入到序列ints[]中, 否则分别将区间
加入到序列ints[]中, 否则分别将区间![[0, \alpha] [0, \alpha]](http://matrix.is-programmer.com/user_files/Matrix/epics/d3df8d55edf31aea0efcdf495bb0f072428ef4d6.png) ,
, ![[\beta, 2\pi] [\beta, 2\pi]](http://matrix.is-programmer.com/user_files/Matrix/epics/366a660a7f4ef9b35c01ce93bc1efe8873352478.png) 加入到序列ints[]中.
加入到序列ints[]中.
(4) 将区间序列ints[]按左端排序, 合并各个相交的区间;
(5) 最后剩下的不相交区间的长度总和就是所求夹角.
下面为解决这个问题的代码, 函数接口为double angfun(pt p[], int n) , 由于本题光源刚好在原点,所以不当作参数, 对其他点也是容易处理的, 坐标平移一下即可.
-
struct pt{
-
double x, y;
-
};
-
-
struct interval{
-
double a, b;
-
};
-
-
const double pi=acos(-1.0);
-
-
bool cmp(interval s1, interval s2)
-
{
-
return s1.a<s2.a || s1.a==s2.a && s1.b<s2.b;
-
}
-
-
double angle(pt p)
-
{
-
double r, alpha;
-
-
r=sqrt(p.x*p.x+p.y*p.y);
-
alpha=acos(p.x/r);
-
if(p.y<0) alpha=2*pi-alpha;
-
return alpha;
-
}
-
-
double angfun(pt p[], int n)
-
{
-
int i, m=0, t;
-
interval s[110];
-
double a, b, total;
-
-
p[n]=p[0];
-
-
for(i=0; i<n; i++){
-
a=angle(p[i]);
-
b=angle(p[i+1]);
-
if(a>b) swap(a, b);
-
if(b-a<pi-eps){
-
s[m].a=a;
-
s[m].b=b;
-
m++;
-
}
-
else{
-
s[m].a=0;
-
s[m].b=a;
-
m++;
-
s[m].a=b;
-
s[m].b=2*pi;
-
m++;
-
}
-
}
-
-
sort(s, s+m, cmp);
-
-
t=0;
-
for(i=1; i<m; i++)
-
if(s[i].a<=s[t].b){
-
if(s[t].b<s[i].b) s[t].b=s[i].b;
-
}
-
else s[++t]=s[i];
-
-
total=0;
-
for(i=0; i<=t; i++) total+=s[i].b-s[i].a;
-
-
return total;
-
}
-
讨论: 假设允许点在多边形上, 这个方法也是可用的, 不过我们需要知道这个时候点是看作影响多边形外还是影响多边形内. 另外还需要判断每条边的左侧是内部还是右侧是内部. 这只要按叉积求一次面积即可判断. 具体在此从略. 本部分感谢bigheadghost提示.
PS: PKU上该题做成多case会wrong到死, 要做成单case才能过, 晕死!
