World Final 2008 Problem B -- 判断多项式恒被整除
by F.Yang
ACM/ICPC World Final 2008 Problem B 给定整系数多项式  及正整数
及正整数 . 判断对
. 判断对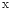 取遍所有整数,
取遍所有整数,  是否恒被
是否恒被 整除.
整除.
分析 我们先定义一些概念.
定义1 设 为整系数多项式,
为整系数多项式,  为非零整数, 若对任意
为非零整数, 若对任意 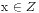 , 都有
, 都有 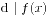 . 我们则称
. 我们则称  恒被
恒被  整除.
整除.
定义2 记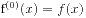 ,
, 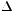 为向前差分算子, 定义n 阶差分多项式(简称n 阶差分)
为向前差分算子, 定义n 阶差分多项式(简称n 阶差分)
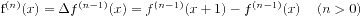 .
.
我们有如下定理.
定理1 整系数多项式  恒被
恒被 整除, 当且仅当
整除, 当且仅当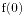 被
被 整除, 且
整除, 且 的一阶差分
的一阶差分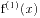 恒被
恒被 整除.
整除.
证明 充分性. 因为 恒被
恒被 整除, 所以
整除, 所以 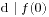 ,
, 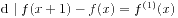 (
(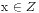 ). 充分性得证.
). 充分性得证.
必要性. 使用数学归纳法. 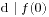 . 设对非负整数数
. 设对非负整数数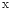 , 都有
, 都有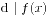 . 又因为
. 又因为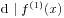 , 故
, 故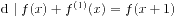 . 同理, 设对整数
. 同理, 设对整数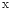 , 有
, 有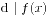 . 则
. 则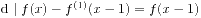 . 综合上述, 由数学归纳法知, 必要性得证.
. 综合上述, 由数学归纳法知, 必要性得证. 
定理2 设整系数多项式 的次数为
的次数为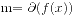 , 则
, 则 恒被非零整数
恒被非零整数 整除, 当且仅当
整除, 当且仅当 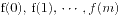 均被
均被 整除.
整除.
证明 充分性是显然的.
必要性的证明施归于纳多项式的次数m. 当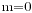 , 即
, 即 为常数时, 结论显然成立. 设
为常数时, 结论显然成立. 设 时结论成立. 则对
时结论成立. 则对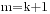 次多项式
次多项式 , 若
, 若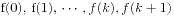 均被
均被 整除, 则
整除, 则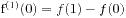 ,
, 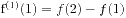 , ... ,
, ... , 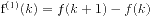 均能被
均能被 整除。又有
整除。又有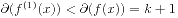 . 由归纳假设知, 一阶差分
. 由归纳假设知, 一阶差分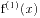 恒被
恒被 整除. 又根据定理1, 得知
整除. 又根据定理1, 得知 恒被
恒被 整除. 由数学归纳法, 必要性得证.
整除. 由数学归纳法, 必要性得证. 
定理3 设整系数多项式 的次数为
的次数为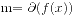 , 则
, 则 恒被非零整数
恒被非零整数 整除, 当且仅当对任意连续m+1个整数
整除, 当且仅当对任意连续m+1个整数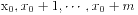 , 有
, 有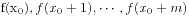 均被
均被 整除.
整除.
定理3作为定理2的推广, 证明方法也是类似的, 此处从略.
推论1 设整系数多项式 的次数为
的次数为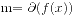 ,
, 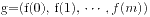 ,
,  恒被
恒被 整除当且仅当
整除当且仅当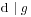 .
.
至此,整个问题得到完整解决.
