Welcome to Matrix's Garden

Google Code Jam Round1A "Number"

by 小伟

Google Code Jam Round1A "Number"

题目描述：给定一个数n（2 <= n <= 2000000000），求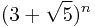 $$$(3+\sqrt{5})^n$ 的整数部分最后三位。

For example, when n = 5, 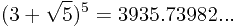$(3+\sqrt{5})^5 = 3935.73982...$ The answer is 935.

解法：

1. 直接求，要求精度高，当n>28时，结果就出错。

2. 技巧解法，配数法：

首先设

$F(X)=\lfloor(3+\sqrt{5})^x\rfloor$

$G(X)=(3+\sqrt{5})^x+(3-\sqrt{5})^x$

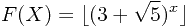
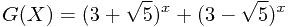
把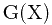 G(X) 展开，得到：

$G(X)=\sum_{i=0}^{x}(3)^{x-i}(\sqrt{5})^i+\sum_{i=0}^{x}(3)^{x-i}(\sqrt{5})^i(-1)^i$

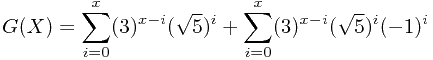
展开后发现，包含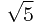 $\sqrt{5}$ 的项都相互抵消了，得到：

$G(X)=\sum_{i=0}^{x/2}3^{(x-2*i)}5^{i}$

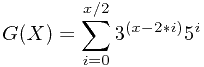
从上式中可以看出，G(X)是整数。

由于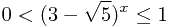 $$$0<(3-\sqrt{5})^x\leq1$ ，因此 $$F(X)=G(X)-1$$ 。

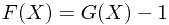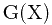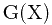于是问题就转化为求 G(X) ，求 G(X) 也是使用配数法，如下：

$6\times G(X)=G(X)\times(3+\sqrt{5})+G(X)\time(3-\sqrt{5})$$$

$=\lbrack(3+\sqrt{5})^x+(3-\sqrt{5})^x\rbrack\times(3+\sqrt{5})+\lbrack(3+\sqrt{5})^x+(3-\sqrt{5})^x\rbrack\times(3-\sqrt{5})$$$

$=\lbrack(3+\sqrt{5})^{x+1}+(3-\sqrt{5})^{x+1}\rbrack+4\times\lbrack(3+\sqrt{5})^{x-1}+(3-\sqrt{5})^{x-1}\rbrack$

$=G(x+1)+4\times G(x-1)$

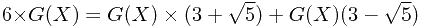
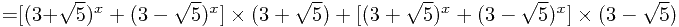
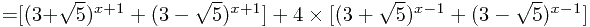
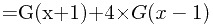
因此，得到递推公式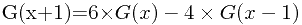 $G(x+1)=6\times G(x)-4\times G(x-1)$

由于题目中的n值较大，不能直接使用递推公式，我们可以构造一个矩阵来加速求解：

$$$\begin{bmatrix}G(x+1)\\G(x)\end{bmatrix}=\begin{bmatrix}6 & -4\\1 & 0\end{bmatrix}\begin{bmatrix}G(x)\\G(x-1)\end{bmatrix}$

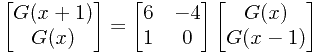
其中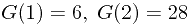 $$$G(1)=6, \;G(2)=28$ ，所以

$$$\begin{bmatrix}G(x+1)\\G(x)\end{bmatrix}=\begin{bmatrix}6 & -4\\1 & 0\end{bmatrix}^{x-1}\begin{bmatrix}G(2)\\G(1)\end{bmatrix}$

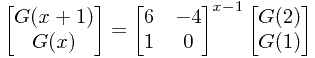
使用按位乘法，就可以在Log(x)的复杂度内，求出G(X)。

至此，本题顺利解决。

Google Code Jam Round1A "Number"

Matrix

分类

最新评论

最新留言

友情链接

功能

浏览计数器