by F.Yang     

      CII-2187问题描述：一人以看录像维生.  每个录像有三个属性 (s, f, p) 分别表示该任务的开始时间，结束时间和所得收入. 但这个人在同一时刻最多只能看两个录像. 现给定 n 个录像. 问这个人的最大收入是多少.

      分析： 我们把问题一般化, 设这个人在同一时刻最多能看 k 个电影. 我们使用最小费用最大流来解决这个问题.

      把每个任务的开始时间和结束时间都对应设为图的一个顶点. 对每个任务 (s, f, p), s 结点到 f 结点连一条弧, 容量为1, 费用为 -p. 而对任意两个任务(si, fi, pi), (sj, fj, pj), 如果fi<=sj, 则从 fi 到 sj 连一条弧, 容量为1, 费用为0. 设一超级源 R0, R0 到各个任务的开始时间 si 都连一条容量为1, 费用为0的弧. 再设一超超级源 R1, R1仅有到R0容量为k, 费用为0的弧. 最后设一超级汇 R2, 各任务的结束时间 fi 到R2都有一条容量为1, 费用为0的弧.

      求从 R1 到 R2 的最小费用最大流, 得到费用 cost, 则 -cost 即为问题的答案.

      讨论： 虽然上述算法在一般化的角度解决了这个问题, 但是由于解决费用流的算法复杂度约为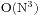, 这在某些有特殊限制的问题变种里并不见得是一种首选的高效算法. 现在总结一下一些特殊的变种及适合的方法.

      (1) 单资源无费用. 如果上题那个人任一时刻只能看一个录像, 并且每看一个录像的收入都是1, 那么这是一个经典的活动安排问题. 任务按结束时间排序后使用贪心算法即可解决. 算法的时间复杂度为.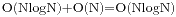

      (2) 单资源有费用. 如果上题观看者每一时刻都只能看一个录像. 任务按结束时间排序后使用一个DP即可, 设 dp[i] 表示以任务 i 结束的情况下所能获得的最大收益. 该算法的时间复杂度为.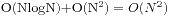

      (3) 多资源无费用. 如果上题里观看者每一时刻最多可以看k个录像, 但是看每个录像的收入都是1. 可以使用如下算法解决:
      a. 维护一个数据结构T, 表示各个资源的最后可用时间, 初始时里面有k个0;
      b. 将任务按结束时间排序; 
      c. 顺序扫描每个任务 (s, f), 在 T 里面查找一个不大于 s 的最大的元素 t. 如果能找到, 则选取该任务, 并将 t 更新为 f 加入回 T 中, 若不能找到 t, 则放弃该任务.
      T使用平衡树来维护, 每次查找和更新的复杂度为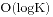, 整个算法的复杂度为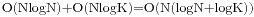. 但编码的复杂度很大.

      (4) 两资源有费用. 这即为原题本身. 可以使用两维状态的三方dp来解决. 小伟已经使用该方法通过了该题. 呼唤小伟给出算法详解和代码.